The recursive model index, a learned index structure

Last update: Dec 27, 2022

Related tags

Overview

RMI

This is a reference implementation of recursive model indexes (RMIs). A prototype RMI was initially described in The Case for Learned Index Structures by Kraska et al. in 2017.

RMI basics

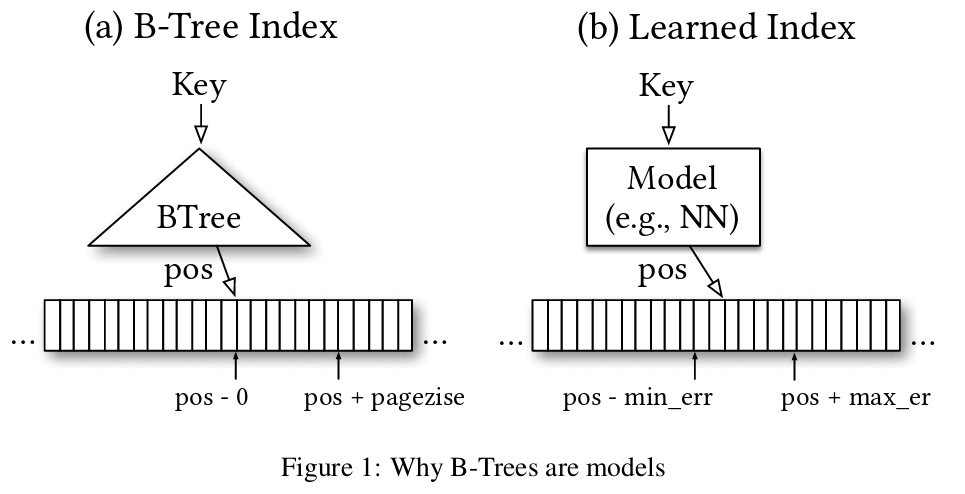
Like binary search trees, an RMI is a structure to help search through sorted data. Given a sorted array, an RMI is a function that maps a key to an approximate index. This approximate index can be used as a starting point for a linear, exponential, or binary search. The SOSD benchmark demonstrates that RMIs can outperform binary search and many other standard approaches as well.

Unlike a binary search tree, an RMI uses machine learning techniques to build this approximation function. The result is normally a small, compact mathematical function that can be evaluated quickly. RMIs are a good tool when you need to search the same sorted data many times. Compared to other structures, RMIs:

( ➕ ) Offer faster lookup times (when properly tuned)
( ➕ ) Are generally much smaller than traditional structures like B-Trees or radix trees
( ➖ ) Must be trained ahead of time on a dataset
( ➖ ) Do not support inserts (without retraining the model)

Many more details can be found in the original paper.

Using this implementation

To use the reference implementation, clone this repository and install Rust.

The reference RMI implementation is a compiler. It takes a dataset as input, and produces C/C++ source files as outputs. The data input file must be a binary file containing:

The number of items, as a 64-bit unsigned integer (little endian)
The data items, either 32-bit or 64-bit unsigned integers (little endian)

If the input file contains 32-bit integers, the filename must end with uint32. If the input file contains 64-bit integers, the filename must end with uint64. If the input file contains 64-bit floats, the filename must end with f64.

In addition to the input dataset, you must also provide a model structure. For example, to build a 2-layer RMI on the data file books_200M_uint32 (available from the Harvard Dataverse) with a branching factor of 100, we could run:

cargo run --release -- books_200M_uint32 my_first_rmi linear,linear 100

Logging useful diagnostic information can be enabled by setting the RUST_LOG environmental variable to trace: export RUST_LOG=trace.

Generated code

The RMI generator produces C/C++ source files in the current directory. The command directly above, for example, produces the following output. The C/C++ sources contain a few publicly-exposed fields:

#include <cstddef>
#include <cstdint>
namespace wiki {
    bool load(char const* dataPath);
    void cleanup();
    const size_t RMI_SIZE = 50331680;
    const uint64_t BUILD_TIME_NS = 14288421237;
    const char NAME[] = "wiki";
    uint64_t lookup(uint64_t key, size_t* err);
}

The RMI_SIZE constant represents the size of the constructed model in bytes.
The BUILD_TIME_NS field records how long it took to build the RMI, in nanoseconds.
The NAME field is a constant you specify (and always matches the namespace name).
The load function will need to be called before any calls to lookup. The dataPath parameter must the path to the directory containing the RMI data (rmi_data in this example / the default).
The lookup function takes in an unsigned, 64-bit integer key and produces an estimate of the offset. The err parameter will be populated with the maximum error from the RMI's prediction to the target key. This lookup error can be used to perform a bounded binary search. If the error of the trained RMI is low enough, linear search may give better performance.

If you run the compiler with the --no-errors flag, the API will change to no longer report the maximum possible error of each lookup, saving some space.

uint64_t lookup(uint64_t key);

RMI Layers and Tuning

Currently, the following types of RMI layers are supported:

linear, simple linear regression
linear_spline, connected linear spline segments
cubic, connected cubic spline segments
loglinear, simple linear regression with a log transform
normal, normal CDF with tuned mean, variance, and scale.
lognormal, normal CDF with log transform
radix, eliminates common prefixes and returns a fixed number of significant bits based on the branching factor
bradix, same as radix, but attempts to choose the number of bits based on balancing the dataset
histogram, partitions the data into several even-sized blocks (based on the branching factor)

Tuning an RMI is critical to getting good performance. A good place to start is a cubic layer followed by a large linear layer, for example: cubic,linear 262144. For automatic tuning, try the RMI optimizer using the --optimize flag:

cargo run --release -- --optimize optimizer_out.json books_200M_uint64

By default, the optimizer will use 4 threads. If you have a big machine, consider increasing this with the --threads option.

The optimizer will output a table, with each row representing an RMI configuration. By default, the optimizer selects a small set of possible configurations that are heuristically selected to cover the Pareto front. Each column contains:

Models: the model types used at each level of the RMI
Branch: the branching factor of the RMI (number of leaf models)
AvgLg2: the average log2 error of the model (which approximates the number of binary search steps required to find a particular key within a range predicted by the RMI)
MaxLg2: the maximum log2 error of the model (the maximum number of binary search steps required to find any key within the range predicted by the RMI)
Size (b): the in-memory size of the RMI, in bytes.

Citation and license

If you use this RMI implementation in your academic research, please cite the CDFShop paper:

Ryan Marcus, Emily Zhang, and Tim Kraska. 2020. CDFShop: Exploring and Optimizing Learned Index Structures. In Proceedings of the 2020 ACM SIGMOD International Conference on Management of Data (SIGMOD '20). Association for Computing Machinery, New York, NY, USA, 2789–2792. DOI:https://doi.org/10.1145/3318464.3384706

If you are comparing a new index structure to learned approaches, or evaluating a new learned approach, please take a look at our [benchmark for learned index structures](https://learned.systems/sosd.

For RMIs and learned index structures in general, one should cite the original paper:

Tim Kraska, Alex Beutel, Ed H. Chi, Jeffrey Dean, and Neoklis Polyzotis. 2018. The Case for Learned Index Structures. In Proceedings of the 2018 International Conference on Management of Data (SIGMOD '18). Association for Computing Machinery, New York, NY, USA, 489–504. DOI:https://doi.org/10.1145/3183713.3196909

This work is freely available under the terms of the MIT license.

Contributors

Ryan Marcus

Comments

Multiple layers

Trying to train with three layers fails:

cargo run --release -- books_200M_uint32 my_first_rmi linear,linear,linear 100
    Finished release [optimized + debuginfo] target(s) in 0.02s
     Running `target/release/rmi /z/downloads/books_200M_uint32 my_first_rmi linear,linear,linear 100`
thread 'main' panicked at 'explicit panic', <::std::macros::panic macros>:2:4
note: run with `RUST_BACKTRACE=1` environment variable to display a backtrace

Is this because of an intentional limitation on the number of layers or some other issue?

opened by r-barnes 3

Optimizer interpretation
Any thoughts on how to interpret the output of the optimizer? I'm seeing a table with entries

Models Branch AvgLg2 MaxLg2 Size (b)

But I haven't found an explanation of what these mean.
opened by r-barnes 2
cleanup() should only be called on malloc'ed model parameters
Hi, I just trained a model with two linear_spline layers and a branching_factor of 200,000, i.e.

cargo run --release -- somedata_100M_uint64 sosd_rmi linear_spline,linear_spline 200000

The resulting C++ program does not compile with the following error:

sosd_rmi.cpp:11:5: error: no matching function for call to 'free' free(L1_PARAMETERS); ^~~~ /Applications/Xcode.app/Contents/Developer/Platforms/MacOSX.platform/Developer/SDKs/MacOSX10.15.sdk/usr/include/malloc/_malloc.h:42:7: note: candidate function not viable: no known conversion from 'const double [400000]' to 'void *' for 1st argument void free(void *); ^ 1 error generated.

It seems like in the cleanup() function, free is called on L1_PARAMETERS although it was not allocated with malloc.

Looking at codegen::generate_code() free_code should possibly only be generated in case storage has value StorageConf::Disk(path), not in case of StorageConf::Embed.
opened by marcelmaltry 2
NN model support

I noticed that more complex NN models could be used in the paper powered by TensorFlow. But there are only simple models here? How can I build an RMI with a more complex NN model? @RyanMarcus @anikristo

opened by JiTao3 1
[AirIndex Issue 9] Add reload script and update main.cpp
This PR is related to this issue and mainly consists of three modifications:

Add a reload script optimizer.sh. It is used to run the auto-tuning optimizer on SOSD dataset.

Update main.cpp to check if the RMI index is equal to the expected answer.

Update main.cpp to print metrics at each milestone.
opened by pseudoinverse 0
Off-by-one-Error in `train_two_layer` implementation
Hi,

I encountered an assert issue when training RMI on very small (100 items) datasets for testing purposes:

thread '<unnamed>' panicked at 'start index was 100 but end index was 100', [...]/RMI/rmi_lib/src/train/two_layer.rs:27:5

Upon closer investigation, I think I have found an off-by-one error in the train_two_layer function implementation. I did not take a look at the context beyond the function, therefore take what I am about to say with a grain of salt:

Link to source file

The value of split_idx is calculated here:

https://github.com/learnedsystems/RMI/blob/5fdff45d0929beaccf6bc56f8f4c0d82baf10304/rmi_lib/src/train/two_layer.rs#L132

split_idx should be in the interval [0, md_container.len())

https://github.com/learnedsystems/RMI/blob/5fdff45d0929beaccf6bc56f8f4c0d82baf10304/rmi_lib/src/train/two_layer.rs#L139

Now lets look at the case where split_idx == md_container.len() - 1, which is valid per [2.]:

The else branch is taken, since split_idx < md_container.len()

https://github.com/learnedsystems/RMI/blob/5fdff45d0929beaccf6bc56f8f4c0d82baf10304/rmi_lib/src/train/two_layer.rs#L147

split_idx + 1 (== md_container.len()) is passed to build_models_from as start_idx

|| build_models_from(&md_container, &top_model, layer2_model, split_idx + 1, md_container.len(), split_idx_target, second_half_models)

fn build_models_from<T: TrainingKey>(data: &RMITrainingData<T>, top_model: &Box<dyn Model>, model_type: &str, start_idx: usize, end_idx: usize, first_model_idx: usize, num_models: usize) -> Vec<Box<dyn Model>>

Link 4.1

Link 4.2

Assert fails, since md_container.len() > md_container.len() is false

assert!(end_idx > start_idx, "start index was {} but end index was {}", start_idx, end_idx );

Link 5

An obvious fix would be to change the condition in [3.] to split_idx >= md_container.len() - 1, however I am not entirely certain whether that leads to issues in other contexts. I guess a similar issue would happen if similar_idx == 0, only for the first call. I changed the condition in my local version and re-ran the tests - it seems to work just fine:

Running test cache_fix_osm Test cache_fix_osm finished. Running test cache_fix_wiki Test cache_fix_wiki finished. Running test max_size_wiki Test max_size_wiki finished. Running test radix_model_wiki Test radix_model_wiki finished. Running test simple_model_osm Test simple_model_osm finished. Running test simple_model_wiki Test simple_model_wiki finished. ============== TEST RESULTS =============== python3 report.py PASS cache_fix_osm PASS cache_fix_wiki PASS max_size_wiki PASS radix_model_wiki PASS simple_model_osm PASS simple_model_wiki

I can open a pull request with that fix if you would like.
opened by Jonas-Heinrich 0
Clean up generated code

Add #pragma once header guards to C++ output - this is the primary syntactic change as it allows for safe inclusion of the generated headers in multiple files. Clean up generated code by adding some spacing and sorting includes - makes generated code (slightly) easier to read. Update contributors.

A side-effect of the PR is to eliminate trailing whitespace in the touched files.

opened by r-barnes 0
Radix root model not working with small branching factor
Hi, I recently tried to build a model with a radix layer and noticed that radix models do not work with small branching factors (1, 2, 3), e.g.

cargo run --release -- uniform_dense_200M_uint64 sosd_rmi radix,linear 1

I always get an error similar to this:

thread '<unnamed>' panicked at 'Top model gave an index of 2954937499648 which is out of bounds of 2. Subset range: 1 to 200000000', /private/tmp/rust-20200803-28615-1977jkb/rustc-1.45.2-src/src/libstd/macros.rs:16:9

I suspect that the issue stems from models::utils::num_bits. I guess you are computing the amount of bits that are needed to represent the largest index (while loop) and then substract 1 to ensure that the radix model always predicts an index smaller than the branching_factor. However, your implementation appears to be off by 1, i.e. the additional nbits -= 1 is not needed.
opened by marcelmaltry 2

Owner

Learned Systems

Learned systems, machine learning for systems.

GitHub

I will be attempting Advent of Code 2022 with Rust, a language I have never learned before.

Advent of Code 2022 This year, I will be attempting Advent of Code with Rust, a language I have never learned before. I will also be taking some notes

4 Jan 7, 2023

A fast, simple, recursive content discovery tool written in Rust.

A simple, fast, recursive content discovery tool written in Rust ?? Releases ✨ Example Usage ✨ Contributing ✨ Documentation ?? ?? What the heck is a f

3.6k Dec 30, 2022

This tool is for those who often want to search for a string deeply into a directory in recursive mode, but not with the great tool: grep, ack, ripgrep .........一个工具最大的价值不是它有多少功能，而是它能够让你以多快的速度达成所愿......

SSS - so stupid search tool <阿Q的哥锐普> English Documentation install install from source code 1.install rust toolchain curl --proto '=https' --tlsv1.2 -